3. 일상 언어 문장을 술어논리 형식언어 문장으로 번역하기
자연언어는 소위 일상언어를 가리키며, 논리학에서 인공언어는 형식언어를 가리킨다. 우리는 이 장에서 아리스토텔레스 논리학에서 살펴보았던 4가지 형식의 범주 문장을 술어논리의 인공언어를 동원하여 수학적 기호로 표현할 것이다.
A: (∀x)(Sx ⇒ Px) ≡~(∃x)(Sx&~Px)
모든 x에 대하여, S이면 P이다. ≡ S이면서 P가 아닌 x는 없다.
E:(∀x)(Sx ⇒ ~Px) ≡~(∃x)(Sx&Px)
모든 x에 대하여, x가 S이면 P가 아니다. ≡ S이면서 P인 x는 없다.
I: (∃x)(Sx&Px)
S이면서 P인 x가 적어도 하나 있다.
O: (∃x)(Sx&~Px)
S이면서 P가 아닌 x가 적어도 하나 있다.
이항술어를 사용할 때, 가령 "x가 y를 사랑한다"를 표현하기 위해서 우리는 Lxy로 표기할 것이다. 하지만 교환법칙으로써 Lyx는 여기서 성립하지 않는다. 그 이유는 대상 간에 성립되는 관계 방향이 달라지기 때문이다. 또한 여기서 논의역을 세계 전체에 있는 모든 대상으로 정할 수도 있고, 맥락에 따라 사람만으로 한정시킬 수도 있다. 아래의 두 예시를 비교해보며 이해를 더해보자.
"모든 사람 각각에 대하여, 그가 좋아하는 사람이 적어도 한 사람 있다."
(∀x)(∃y)Lxy: For all x, there are some y such that x loves y.
여기서, 논의역을 "모든 사람들의 집합"으로 한정한다면, 식은 아래와 같이 변할 것이다.
Hx: x는 사람이다. 를 추가해보자.
≡ (∀x)(∃y)(Hx→(Hy&Lxy)
≡ (∀x)(Hx→(∃y)(Hy&Lxy)
그렇다면, 위 문장은 "모든 사람들이 사랑하는 사람이 적어도 한 사람 있다."를 뜻하게 될 것이다. 반면, 아래와 같이 두 양화사의 위치를 바꿀 시 문장은 전혀 다른 문장을 의미하는 것을 알 수 있다.
(∃y)(∀x)Lxy: There are some y such that, for all x, Lxy.
그러니까, 모든 x는 적어도 한 명의 y를 사랑한다는 뜻이 되므로 앞의 문장과는 전혀 다른 뜻이 된다는 것을 알 수 있다. 이로써, 우리는 둘째 문장이 첫째 문장의 수동태로 바꾼 것에 지나지 않는 표현임에도 불구하고 그 의미가 전혀 다른 것을 뜻한다는 것을 알았다. 일상언어가 어떠한 경우에서 논리적 의미를 온전히 보존하지 못한다는 것을 나타내는 대목이다.
다음의 문장을 술어논리의 언어로 번역해보자.
1. 현명한 사람들만이 관용을 베풀 줄 안다.
x는 현명한 사람이다: Wx
관용을 베풀 줄 안다: Bx
"S만이 P이다."는 명제는 "S가 아닌 것은 모두 P가 아니다"와 같은 의미를 지닌다. 따라서
(∀x)(Wx⇒Bx) 로 표현할 수 있다.
2. 수업에 참여하지 않은 모든 학생들은 아프거나 소풍을 갔다.
여기서 논의역을 학생으로 잡는다면,
x는 수업에 참여했다. Ax
x는 아프다 Ix
x는 소풍을 갔다 Px
정도가 필요할 것이다. 그렇다면 번역은 아래와 같이 표현될 수 있다.
(∀x)(~Ax⇒(Ix V Px))
이제 논의역에 사람, 나무와 같은 구체적인 대상뿐만 아니라 시간(time),날(day), 수(number)와 같은 추상적 대상들도 포함시켜야 하는 문장을 번역해보자.
3. 매일 자동차 사고로 다치는 사람이 존재한다.
x가 y(어떠한 날)에 자동차 사고로 다치다: Cxy
x는 사람이다. Hx
y는 날이다. Dy
(∀y)(Dy⇒(∃x)(Hx & Cxy))
위 문장에서 x의 존재양화사를 사용한 이유는 우리가 Cxy에서 x가 사람이고 y가 날day이라는 구분을 약정하고 있는 것이 아니기 때문이다. 따라서 3의 문장에서 "~는 사람이 존재한다"를 표현하기 위해서 우리는 x의 존재양화사를 사용하여 그 의미를 분명히 해주어야 한다.
마지막으로 현대분석철학사에서 중요한 역할을 했던 다음의 문장을 번역해보자. 이 문장은 술어논리의 창시자인 프레게와 분석철학 발전에 큰 기여를 했던 러셀간에 논쟁을 일으켰으며, 비록 이 논의에서 러셀의 주장이 더 많은 지지를 받았지만, 이로 하여금 우리는 하나의 명사가 순전히 하나의 기호로 표현되어야 하는 것이 아님을 알 수 있다.
4. 프랑스의 현재 왕은 대머리이다.
The present king of France is bald.
프레게는 프랑스의 현재 왕을 특정 기술구definite description으로 여겼기 때문에 이를 단순히 고유명사로 간주했다. 그리고 그러할 때 고유명사가 지칭하는 대상(프랑스의 현재 왕)이 존재하지 않으므로 - 2월 혁명 이후 나폴레옹이 대통령으로 취임한 뒤 프랑스에서 더 이상의 왕은 없었다. 위 논의는 1800년대 후반에 벌여진 논쟁이다. - 위 문장에 대한 참, 거짓 판별은 불가능하다고 여겼다. 반면, 러셀은 특정 기술구를 대상을 지칭하는 표현이 아닌 "술어를 지칭하는 표현, 존재를 나타내는 표현, 유일성을 나타내는 표현"으로 나누어진다고 여겼다. 앞서 언급했듯이, 번역 시 가장 유의해야 할 점은 우선 문장 전체의 의미를 사태situation적이고 논리적으로 파악해야 하기 때문이다.
그렇다면 위 문장은 3가지 의미를 갖고 있다.
4.1. 프랑스의 현재 왕은 존재한다.
4.2. 프랑스의 현재 왕은 기껏해야(많아야) 한 사람이다.
4.3. 그 자는 대머리이다.
이 3가지 의미를 술어논리의 언어로써 한 문장에 담으면 다음과 같다.
논의역: 사람들의 집합
Fx: x는 프랑스의 현재 왕이다
Bx: x는 대머리이다.
4. 프랑스의 현재 왕은 대머리이다.
The present king of France is bald.
(∃x)(Fx&(∀y)(Fy⇒(y=x))&Bx)
여기서 의문이 들 수 있는 점은 Fy⇒(y=x) 일 수 있는데, 이는 4.2를 번역한 것이다. 즉, 프랑스의 현재 왕이 설령 y로 간주될지라도, 프랑스의 현재 왕은 기껏해야 한 사람이기 때문에, x가 아닌 다른 y는 x와 같아야 한다. 우리는 위 번역된 언어를 권병진 박사의 만족표를 통하여 타당성을 검사해볼 것이다. 이는 아래와 같은 방법으로 검사할 수 있다.

우리는 위 만족표로부터 4.2에서 나타난 프랑스 현재 왕의 고유성의 의미를 타당하다고 밝혔으며 이로부터, "프랑스의 현재 왕은 대머리이다." 라는 문장은 타당하다는 것을 도출하였다.
4. 술어논리의 의미론
(1) 형식언어로 표현된 문장의 해석
형식언어로 표현된 문장은 해석이 주어지기 전에는 아무런 의미를 갖고 있지 않다. 해석interpretation은 형식언어에서의 문장에 의미를 부여하는 일을 뜻하는데, 그럼으로써 일상언어 문장이 갖는 의미를 형식언어 문장에 부여할 수도 있을 것이다. 그러나 이에 관한 "더 직접적인 방법은" 가능상황을 적어도 형식언어 문장의 비논리적 상항 non-logical constant과 관련되는 범위 내에서 기술함으로써 이들이 가능상황의 관련 요소들과 관계 맺게 하는 것이다. 즉, 다시 형식언어 문장과 가능상황을 관계 맺게 하는 것이다. 이렇게 형식언어 문장에 해석을 주는 순간 그 문장은 의미를 가지면서 T/F를 가질 수 있다. 이에 관한 절차는 다음과 같다.
1. 논의역 설정
2. 1항 술어에는 논의역의 부분집합을, 2항 술어에는 논의역의 원소들의 순서쌍을, 3항 이상의 술어에는 논의역의 원소들을 순서열로써 표현한다.
3. 고유명사에는 논의역의 한 원소를 할당한다. 가령, Ws에서 s={a}이다. 이렇게 어떤 원소를 할당하면 술어논리에서 그 의미를 파악할 수 있다.
4. 명제 상항(문장 상항)에는 진리치를 할당한다.
문장 S는 해석 I 에서 참이다 ≡ 해석 I 에서 모든 (제한된) 순서열이 문장 S를 만족시킨다.
해석 I 에서 고려해야 하는 (제한된) 모든 순서열들이 여러 형식의 열린문장과 닫힌문장을 만족시키는지의 여부를 기계적인 방법으로 점검하는 표가 타르스키 만족표이다. 이로부터 우리는 최종적으로 해석 I 에서 고려해야 할 모든 순서열들을 문장 전체를 만족시키는지 여부에 따라 이 문장의 T/F를 결정할 수 있다. 아래의 예시를 보자.
5. (∀x)(Px ⇒ Qx) 일 때,
논의역이 {a,b,c}이고, P= {a,b,c}, Q={a,b} 라면 문장 5가 해석 I1에서 어떤 진리치를 갖게 되는지 만족표를 이용하여 알아보자.
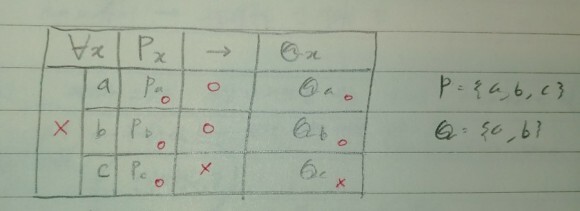
따라서 위 문장은 해석 I1 하에서 거짓이다.
이와 같이 단순한 술어논리 언어 문장 뿐만 아니라 매우 복잡한 문장 또한 일단 해석이 주어지면 우리는 이 해석 하에서 문장의 진리치가 무엇인지 만족표를 통해 알 수 있다.
권병진 박사 강의록 & 강의노트 참고
