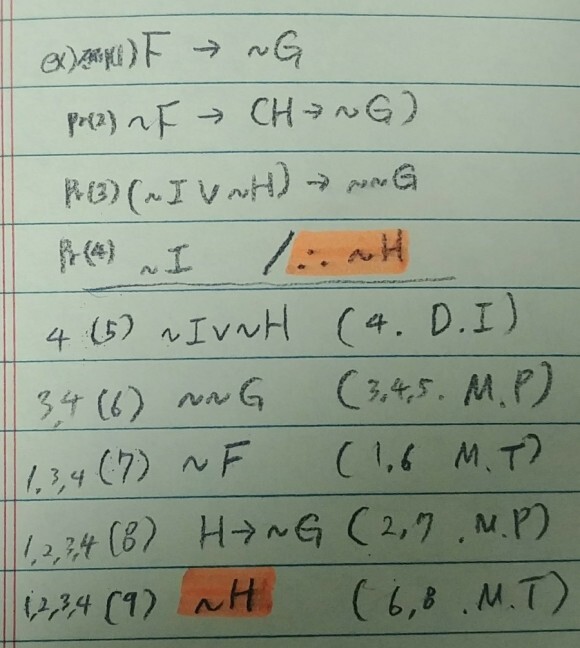구문론syntactics은 언어 자체에 관심을 가진다. 가령, 문법이 그것이다. 의미론semantics은 언어가 어떤 의미를 갖는지에 관심을 가진다. 다시 말해 언어가 의미하는 바를 연구한다.
3. 타당성과 비일관성
타당성은 비일관성과 직접적인 연관성을 가진다. 문장들의 집합 S가 비일관적이다라는 말은 iff 문장들의 집합 S의 원소들인 문장들이 모두 함께 참일 수 없다는 것을 뜻한다. 다시 말해 S의 원소들인 문장들이 모두 함께 참이 되는 논리적 가능상황이 존재하지 않는다는 것을 뜻한다.
그렇다면 집합에 문장A 단 하나만 들어있는 경우는 어떠한가? 문장 A가 참인 논리적 가능상황이 존재하지 않는 경우 그리고 그러한 경우에만 문장 A는 비일관적이다. 이 때 문장A는 모순문장이다. 반면에 어떠한 진리치를 할당하여도 항상 참이 되는 문장은 항진tautology문장이라고 한다. 이 때, 항진문장 단 하나만을 가지고 있는 집합 S는 일관적이다.
그렇다면, 문장들의 집합 S의 비일관성 개념과 타당성 개념은 어떠한 연관을 가질까? 논증 A가 타당하다 iff 논증 A의 전제들과, 결론의 부정으로 이루어진 문장 집합 S가 비일관적이다. 가령, 전제 P1, P2와 결론 C의 논증이 타당하다면, iff {P1, P2, ~C}는 비일관적이다. 또한, {P1, ~C2, ~~P2}가 비일관적일 때, ≡ 전제 P1, ~C, 결론 ~P2 는 타당하다. 단, 집합의 원소는 순서가 없기 때문에, 원소열로부터 논증형으로 변환할 때 전제와 결론의 자리바꿈이 얼마든지 가능하다.
문장들의 집합 S가 비일관적이라면, 즉, S의 원소들인 문장들이 함께 참일 수 없다면, 그 이유는 무엇일까? S의 모든 문장들의 연언(&)이 모순문장으로서 논리적으로 거짓이기 때문이다. 모순문장은 P형식의 문장과 ~P형식의 문장을 논리적으로 함축하고 있기 때문에 모든 진리치 할당에서 거짓이 된다. 아울러, 연언문은 각 연언지가 모두 참이어야 참이 되고, 선언문은 선언지들 중 적어도 하나가 참인 경우에 iff 참이 된다.
동일율: P ⇒ P 항진문장
모순율: P & P 모순문장
배중율 excluded middle: P V ~P 항진문장 (T/F의 중간이 없다)
진리 나무(Truth tree)
진리나무에 대해 간략히 설명하겠다. 사실 이 방법은 그렇게 효율적이지는 않다. 미국에서는 많이 좋아하는 것 같지만, 잘 익혀둔다면 앞장에서 배운 약식 참/거짓 판별법이 더 효율적이다.

위 그림은 진리나무에 의한 타당성 검사 방법이다. 맨 아래에 X 표시는 닫혀있다는 것을 의미하고, X가 없는 것은 열려있다는 것을 의미한다. 열려있다는 것은 각 문장들이 함께 참일 수 있다는 것을 의미한다. 하지만 타당함은 모든 가지가 닫혀있을 때 그리고 그러할 때에만 가능하다. 따라서 위 논증은 부당하다.
그러나 여기서 주의할 점은, 3번행에 있는 문장~(C&A)는 사실 논증에서는 결론으로서 (C&A)를 가리킨다. 진리나무에서 결론 문장에 부정을 취하는 이유는 진리나무가 비일관성 개념에 근거하기 때문이다.
4. 형식적 증명(타당성에 대한 구문론적 검사 방법)
형식적 증명은 논증형식의 전제들로부터 기본적인 추론규칙을 동원하여 결론을 도출하는 것이다. 이는 구문론적 방법인데, 다시 말해 문장 자체의 구조 또는 구성만을 고려하는 것이다. 구문론적 방법은 의미론적 방법과 같은 결과를 낳을 때만 성공적인 검사 방법으로 간주될 수 있다.
형식적 증명 체계는 소위 SC(sentential calculus)라고 일컫기도 한데, 완전한 형식적 증명 체계는 어떤 하나의 형식적 증명 체계가 모든 타당한 논증들을 valid하다고 판별할 때를 가리킨다. 게다가 건전한 형식적 증명 체계는 어떤 하나의 형식적 증명 체계가 valid 하다고 판별한 모든 논증이 실제로도 타당한 것으로 밝혀질 때를 가리킨다.
이러한 SC의 추론규칙은 순수 추론규칙과 대치규칙으로 나누어진다. 형식적 증명은 각 행마다 전제 문장들의 번호, 행 번호, 도출된 문장, 정당화라는 4가지 요소로 이루어져 있다. 형식적 증명에서 우리는 증명에 도움이 되는 경우 어떠한 문장도 임시적으로 전제로 도입하여 도출에 이용할 수 있다. (technical point) 하지만 이렇게 임시적으로 전제로 도입한 문장의 번호는 증명의 마지막 행의 전제 번호에서 제외되어야 한다.
4-A. 순수 추론규칙(타당한 논증형식을 추론규칙으로 만든 것)
1. 전건긍정M.P
2. 후건부정M.T
3. 가언삼단논법H.S hypothetical syllogism
P ⇒Q
Q⇒R
--------
P⇒R
4. 선언삼단논법D.S
P V Q
~P
--------
Q
5. 딜레마
6.흡수논법Abs
P ⇒ Q
---------
P ⇒ (P & Q)
7.단순화Simp or 연언제거 C.E
P & Q
---------
P
8.연언도입C.I
P
Q
------
P & Q
9.선언도입D.I
P
-----
P V Q
10. 부정도입 N.I
전제 (b) Φ
....
b,c,d (n) Ψ & ~Ψ
c,d (o) ~Φ (b,n 부정도입)
(n)행에서 논리적 모순이 일어났는데, 이러할 경우에 그 행의 전제들 중 아무거나, 가령 b행의 문장, 부정을 취하여 o행에 기재한다. 그리고 n행의 전제 번호들 중에서 b를 제거한 나머지 전제번호들을 o행의 전제번호로 기입한다.
11. 조건도입C.I
전제 (b) Φ
...
b,c (j) Ψ
c (k) Φ ⇒ Ψ (조건도입, 6)
j 행의 전제 번호들 중에서 b가 존재한다. 이럴 때 b행의 문장을 전건으로 삼고 j행의 문장을 후건문으로 삼는 조건문을 k행에 쓸 수 있다. 하지만 j행의 전제 번호들 중에서 b를 제거한 나머지 전제 번호들을 k행의 전제 번호로 기입한다.
정당화
Φ={P1,P2,P3 ... Pk, Pn}일 때, Ψ의 논증은 Pk ⇒ C 로 구성된다. 이럴 때,
Φ가 타당하다 iff Ψ가 타당하다. 게다가 만약 Φ가 타당하다면 {P1,P2 ...Pn,~C}는 비일관적이다. 그렇다면, {P1,P2 ... Pn, ~(Pk ⇒C)} 또한 비일관적이다.
12. 선언제거D.E
d (h) Φ V Ψ
전제 (i) Φ
...
f,i (j) Ω
전제 (k) Ψ
...
g,k (l) Ω
d,f,g (m)Ω (h,i,j,k,l. D.E)
맨 앞의 선언문에서 한 선언지를 i에 전제한 뒤, 이로부터 다른 전제 f행 문장을 더불어 사용하여 j행에서 Ω를 도출한다. 그리고 k 행에서 앞 선언문의 다른 선언지 Ψ를 전제한 뒤, 이로부터 다른 전제 g행의 문장을 더불어 사용하여 l행에서 역시 Ω를 도출한다. 그리고 이러할 때, m행에서 전제인 i와 k를 제외한 나머지 전제번호를 기입하면서(=d,f,g) Ω를 도출한다.
4-B. 대치규칙
1. 드모르강 정리
2. 교환법칙
3. 결합법칙
4. 배분법칙
5. 이중부정
6. 대우(Trans. Transposition)
7. 질료적 함축(Material Implication)
(P ⇒Q) ⇔(~P V Q)
8. 질료적 동치(Material Equivalence)
(P ⇔ Q) ⇔ [(P ⇒ Q) & (Q ⇒ P)]
[(P & Q) V (~P & ~Q)]
9. Exportation
[(P & Q) ⇒ R] ⇔ [P ⇒ (Q ⇒ R )]
10. 반복
P ⇔ (P V P)
P ⇔ (P & P)
형식적 증명에 관한 간단한 예제